カルノーの原理
熱機関とは、熱を仕事に変え、循環的に動作しつづける機関である。トムソンの原理が示すように、熱機関がサイクルを繰り返し動作するためには、熱源となる高温熱源と熱の流出先である低温熱源とが必要である。これを一般化すると、下図のようになる。
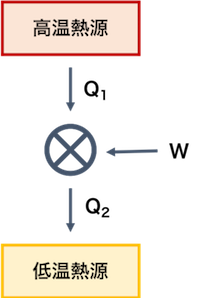
高温熱源から熱 Q1 を取り、その一部を仕事 W として外界に出し、残りの熱 Q2 を低温熱源へ放出するような熱機関を考える。このとき、熱機関を一つの系と見なしたとき、この系において、次のことが成り立つ。
\[ Q_{1} > 0 Q_{2} < 0 W < 0 \]熱力学第 1 法則(エネルギー保存の法則)により、
\[ Q_{1} + Q_{2} + W = 0 \]熱機関の仕事率 e は次のように計算される。
\[ e=\frac{-W}{Q_{1}} = \frac{Q_{1}+Q_{2}}{Q_{1}} \]つまり、高温熱源から流入した熱と、熱機関が外部になされた仕事の比が、仕事効率となる。
カルノーは仕事効率の最大値 emax について研究し、その最大値が熱機関の構造や作業物質によらず、常に高温熱源の温度 Th と低温熱源の温度 Tl のみで決定されることを見出した。これをカルノーの原理といい、次のように数式できる。
\[ e_{max} = F(T_{h} - T_{l}) \]カルノーの原理の証明
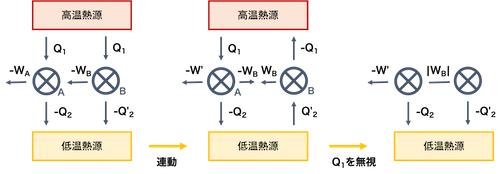
いま、高温熱源 Th で動作する可逆熱機関 A と可逆熱機関 B を考え、それぞれの仕事率を -eA と eB とする。eA < eB と仮定する。また、低温熱源 Tl でも同様な可逆熱機関 A と可逆熱機関 B が動作していると考える。このとき、同じ -Q1 の熱を用いたとき、それぞれの期間が外部にする仕事と低温熱源への放熱は、
\[-W_A=e_AQ_1,-Q_A=(1-e_A)Q_1\] \[-W_B=e_BQ_1,-Q_B=(1-e_B)Q_1\]である。eA < eB だから、
\[ -W_A>-W_B,-Q_A<-Q_B \]ここで、下図のように熱機関 A を正常運動させ、その仕事 WA を用いて熱機関 B を逆運転させる。熱機関 B の逆運転では低温熱源から高温熱源へ熱をくみ上げるには WB の仕事しか必要としない。そこで、-WA > -WB だから
\[ -W_A=-(W_B+W') \]とおける。こうして WA を分割して WB は熱機関 B の逆運転に、W' を外部への仕事として用いることにする。このとき、熱機関 A と熱機関 B を連結して一つの系と見なしたとき、この系は低温熱源から熱をくみ取り外部へ仕事をする第 2 種永久機関となる。これはトムソンの原理に反する。よって、eA ≤ eB である。同様にして、eA ≥ eB も導かれるので、結局 eA = eB となる。