カルノーサイクル | 温度ThとTlで等温膨張、圧縮を行い、その間を断熱膨張、圧縮で結ぶ一連のサイクル

理想気体を作業物質とし、温度 T_h と T_l で等温膨張、圧縮を行い、その間を断熱膨張、圧縮で結ぶ一連の反応をカルノーサイクルという。

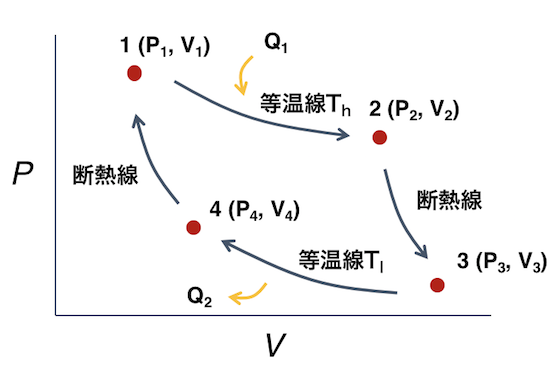
1→2 等温可逆膨張	体積が V₁ → V₂ へと準静的に膨張する。このとき、温度を一定に保つためには、高温熱源 T_h から熱 Q_1→2 を吸収する。
2→3 断熱可逆膨張	体積が V₂ → V₃ へと断熱条件下で準静的に膨張する。このとき、温度は T_h → T_l へと下がる。
3→4 等温可逆圧縮	体積が V₃ → V₄ へと準静的に圧縮する。このとき、温度を一定に保つためには、低温熱源 T_l へ熱 Q_3→4 を放出する。
4→1 断熱可逆圧縮	体積が V₄ → V₁ へと断熱条件下で準静的に圧縮する。このとき、温度は T_l → T_h へと上昇する。

等温可逆膨張 (1 → 2) / 等温可逆圧縮 (3 → 4)

1 → 2、3 → 4 の等温可逆変化では、理想気体のエネルギーは一定に保たれるので、

\[ \Delta U=Q+W=0\Longleftrightarrow Q=-W \]

となる。したがって、系が外界から吸収した熱 Q_1→2 および放出した熱 Q_3→4 は、

\[ \begin{eqnarray} Q_{1\rightarrow2} &=& -W_{1\rightarrow2}=P\Delta V \\ &=& nRT_h\int_1^2\frac{dV}{V} \\ &=& nRT_h\ln\frac{V_2}{V_1} \end{eqnarray} \] \[ \begin{eqnarray} Q_{3\rightarrow4}&=&-W_{3\rightarrow4}=P\Delta V \\ &=& nRT_l\int_3^4\frac{dV}{V} \\ &=& nRT_l\ln\frac{V_4}{V_3} \end{eqnarray} \]

断熱可逆膨張 (2 → 3) / 断熱可逆圧縮 (4 → 1)

内容見直してます。。。。

カルノーサイクルが外界になさる仕事

1 → 2 → 3 → 4 → 1 のひとサイクルによって系が外界にする仕事は、次のように計算される。この仕事は等温線と断熱線で囲まれる面積に等しい。

\[ \begin{eqnarray} -W &=& (-W_{1\rightarrow2})+(-W_{2\rightarrow3})+(-W_{3\rightarrow4})+(-W_{4\rightarrow1}) \\ &=& \mathrm{nR}(T_h-T_l)\ln\frac{V_2}{V_1} \end{eqnarray} \]

また、このときの最大仕事率は、

\[ \begin{eqnarray} e_\max &=& \frac{-W}{Q_{1\rightarrow2}} \\ &=& \frac{Q_{1\rightarrow2}+Q_{2\rightarrow3}+Q_{3\rightarrow4}+Q_{4\rightarrow1}}{Q_{1\rightarrow2}} \\ &=& \frac{T_h-T_l}{T_h} \end{eqnarray} \]

また、可逆カルノーサイクルを逆向きに運転させれば、外部から W の仕事をもらい、低温熱源 T_l より Q_3→4 をくみ上げ、高温熱源 T_h へ Q_1→2 を放出するヒートポンプとして作用する。この場合、ヒートポンプの冷却効果 e_c は次のように計算できる。

\[ \begin{eqnarray} e_c &=& \frac{Q_{3\rightarrow4}}W \\ &=& \frac{Q_{3\rightarrow4}}{-(Q_{1\rightarrow2}+Q_{2\rightarrow3}+Q_{3\rightarrow4}+Q_{4\rightarrow1})} \\ &=& \frac{T_l}{T_h-T_l} \end{eqnarray} \]