外部から外力 Pe(外圧)で、系の気体の体積を dV だけ圧縮させたとき、外部から系になされる仕事 dWe は、次のように計算できる。
\[ dW_{e} = -f(l)dl = -P_{e}Sdl = -P_{e}(V)dV \]気体の体積が V1 から V2 に圧縮されたとき、外部から系になされる仕事 We は、両辺を積分することで求められる。
\[ W_{e} = - \int_{V_{1}}^{V_{2}}P_{e}(V)dV \]有限の速さで系の気体を圧縮させたとき、一般に系の内部の圧力 Pi は外圧に比べ小さい。従って、系が受け取る仕事 Wi は、次のように計算できる。
\[ W_{i} = - \int_{V_{1}}^{V_{2}}P_{i}(V)dV < W_{e} \]熱力学第 1 法則により、We と Wi の差は摩擦などによって、熱 Q に変化する。このとき、系になされた仕事と系が受け取った仕事の間に次のような関係が成り立つ。仕事の一部が熱に変わって、元の状態を復元することができなくなるため、この変化を不可逆変化という。
\[ W_{e} = W_{i} + Q \]不可逆変化に対して、Pe を Pi よりも無限小だけ大きくして、無限に長い時間をかけて変化させる過程を準静的変化という。準静的変化では、仕事が熱に変化しないため、反応は可逆的である。準静的変化のとき、Q = 0 だから、次の式が成立する。
\[ W_{e} = W_{i} \]内部エネルギーの変化
n mol の理想気体がピストン上の質量 m のおもりで体積 V1 の容器に閉じ込められている系を考える。この系における、理想気体が (P1, V1) → (P2, V2) への膨張変化を考える。この際、温度 T を一定に保ち、ピストンの質量を無視できるものとしする。
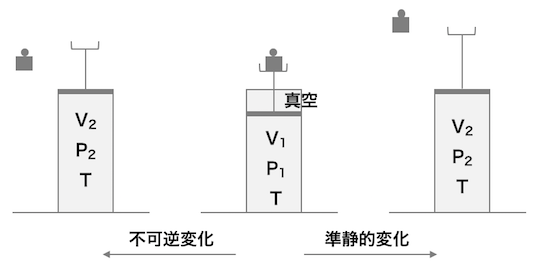
不可逆反応
温度 T において、質量 m のおもりを素早く取り去ると、気体は自由膨張を始め、ピストンの容器の最上部に押し上げられる。理想気体の自由膨張に関してジュールの法則が成り立つので、d'Q = 0 かつ d'W = 0 である。したがって、気体の内部エネルギーの変化は、
\[ \Delta U = d'Q + d'W = 0 \]このとき、理想気体を (P2, V2) &arr; (P1, V1) へと元の状態に戻すには、上から押さなければならない。つまり、W > 0 となる。また、圧縮する際に温度を一定に保つためには外界へ受け取った仕事と同じ量だけ熱 Q 放出していることになる。このとき、
\[ \Delta U = Q + W = (-W) + W = 0 \]となる。こうして気体の自由膨張は不可逆変化となる。
準静的変化(可逆反応)
温度 T において、おもりを無限に分けて、少しずつ取り去る準静的変化では、気体はピストン上にあるおもりを押し上げるので、その仕事は、
\[ W = - \int_{1}^{2}P\Delta V = -nRT\int_{1}^{2} \frac{dV}{V} = -nRT\ln \frac{V_{2}}{V_{1}} \]このとき、温度を一定に保つためには、系は外界から Q = -W の熱を吸収する。また、押し上げられたピストンにおもりをのせて圧縮の際も準静的に行えるから、可逆変化となる。このサイクルを可逆サイクルという。