温度 T において、1 mol の粒子の運動自由度あたりの内部エネルギーは次のように分配できる。
\[ U = \frac{1}{2} RT \]| 分子の形 | 並進運動 | 回転運動 | 自由度 |
| 単原子 | 3 | 0 | 3 |
| 直線 | 3 | 2 | 5 |
| 非直線 | 3 | 3 | 6 |
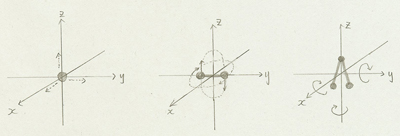
一般に、分子の自由度を ν とすると、1 mol あたりの気体分子の内部エネルギー U は、
\[ U=\frac{\nu}{2}RT+U_0 \]と表せる。U0 は分子に固有の内部エネルギーであり、温度に依存しない。つまり、\( \frac{\partial U_0}{\partial T}=0 \) が成り立つ。この結果を用いて、気体の定積モル熱容量および定圧モル熱容量を次のように書ける。
\[ C_V= \left(\frac{\partial U}{\partial T}\right)_{V} = \frac{\nu}{2}R \] \[ C_P = R + C_V = \frac{\nu+2}{2}R \]