仕事

仕事は、力と変位の積で定義されている。力 f で、物体を微小距離 dl だけ動かしたとき、物体になされる仕事 dW は次のように書ける。

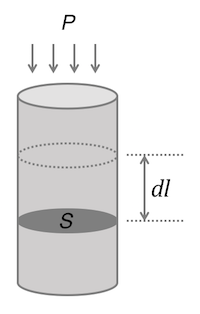
気体が仕事するときは次のように考えることができる。圧力 P で気体を圧縮し、気体を dV だけ減少させたときの仕事を dW とする。図に示したように、圧力が P のとき、気体に加わる力は圧力と断面積の積となるから、f(l) = PS となる。気体が dV だけ減少したとき、ピストンが -dl だけ動いたとすると、気体が受ける仕事（圧力が気体になされた仕事）は、次のように書き表すことができる。

熱力学第 1 法則（エネルギー保存の法則）

ある系を考えたとき、その内部エネルギーは、熱と仕事の和として表され、常に一定となる。この熱と仕事が等価であることは、マイヤーとジュールによって証明されている。

熱力学第 1 法則を微分形で書くと、次のようになる。

d'Q と d'W を不完全微分といい、dU は完全微分と呼ぶ。不完全微分は、状態が変化するとき、その物理量が変遷の経路に影響される。一方、完全微分は状態変化の経路によらない量である。

気体の場合、仕事 W は圧力 P と体積 V で書き表すことができる。