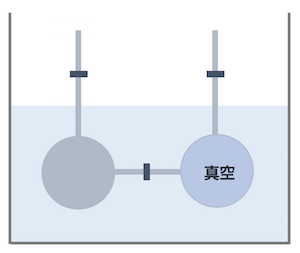
気体の自然膨張では熱が放出されない(Q = 0)。このことについて、ジュールは気体を入れた容器と真空の容器を連結したものを水槽に入れ、コックを開いて気体を自由に膨張させる実験を行って、水槽の水温が変化していないことを見出した。また、水槽に入れた容器の全体の体積が変化しないので、系全体では dV = 0。このとき、仕事は W = -P(V)dV = 0 となる。従って、気体の真空膨張では、内部エネルギーも変化しない。
\[ \Delta U = Q + W = 0 \]
これらの関係を、次のような微分形で書ける。
\[ \left ( \frac{\Delta U}{\Delta V} \right ) T = const. = 0 \]
または、
\[ \left ( \frac{\Delta U}{\Delta P} \right ) T = const. = 0 \]
つまり、温度さえ一定であれば、体積あるいは圧力を変化させても内部エネルギーは変化しない。また、ΔV → 0、ΔP → 0、ΔU → 0 の極限を考えると、上式次のように書ける。
\[ \left ( \frac{\partial U}{\partial V} \right ) T = const. = 0 \]
または、
\[ \left ( \frac{\partial U}{\partial P} \right ) T = const. = 0 \]